1. Задание № 182 

Сложность: I
Классификатор алгебры: Симметрия относительно точки и прямой
Симметрия относительно точки и прямой
i
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно прямой l.
1) 1
2) 2
3) 3
4) 4
5) 5
Решение. Симметрия относительно прямой (или осевая симметрия) — это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону прямой, всегда будет соответствовать точка, расположенная по другую сторону прямой, а отрезки, соединяющие эти точки, будут перпендикулярны оси симметрии и делятся ею пополам.
Фигуры, симметричные относительно прямой l, изображены на рисунке 2.
Правильный ответ указан под номером 2.
Ответ: 2
182
2
Сложность: I
Классификатор алгебры: Симметрия относительно точки и прямой


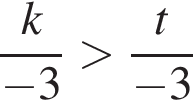
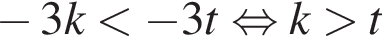 — неверно.
— неверно.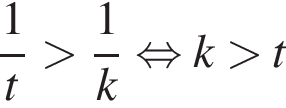 — неверно.
— неверно.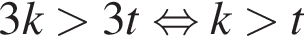 — неверно.
— неверно.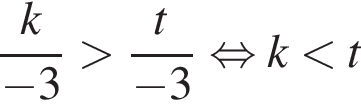 — верно.
— верно. Известно, что
Известно, что 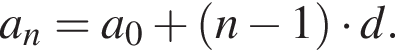 Тогда:
Тогда: 
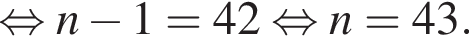
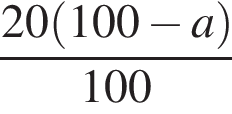
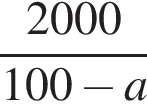
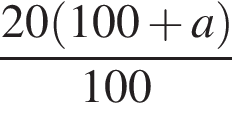
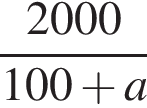
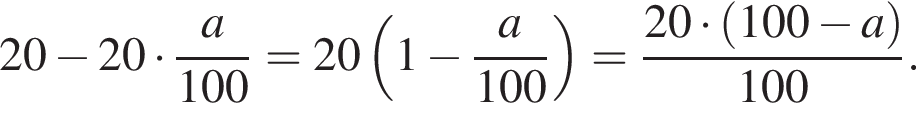
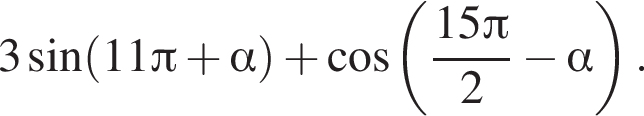
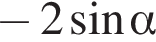



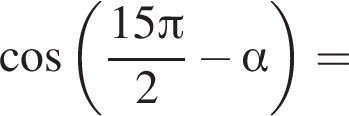
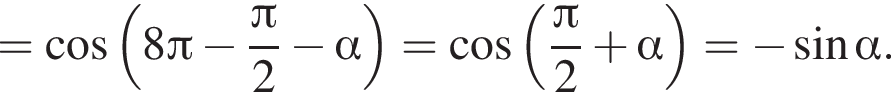
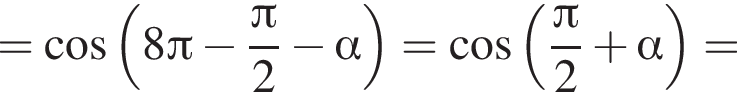
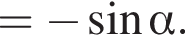
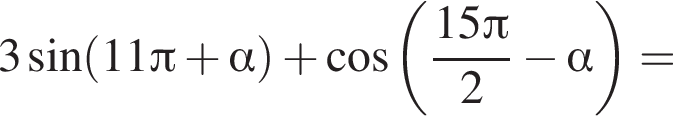

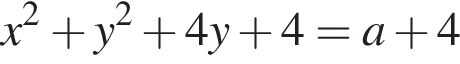 и проходит через вершину параболы
и проходит через вершину параболы 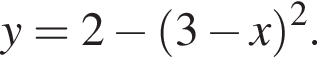 Найдите радиус этой окружности.
Найдите радиус этой окружности.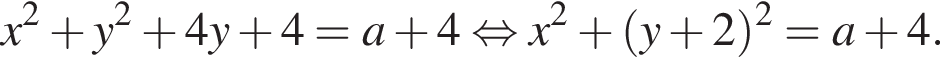
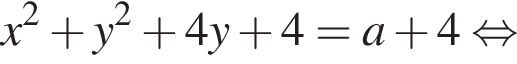
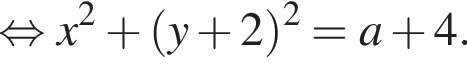
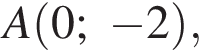 а радиус — это расстояние от точки A до вершины параболы.
а радиус — это расстояние от точки A до вершины параболы.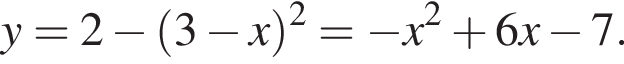
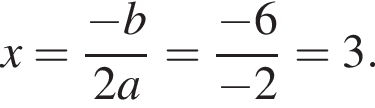 Подставим найденное значение x в изначальное уравнение параболы и получим
Подставим найденное значение x в изначальное уравнение параболы и получим 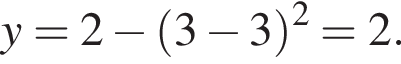 Таким образом, вершина параболы расположена в точке (3; 2).
Таким образом, вершина параболы расположена в точке (3; 2).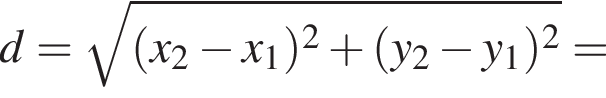
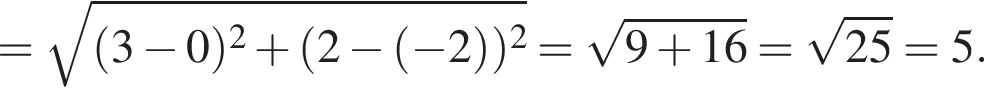
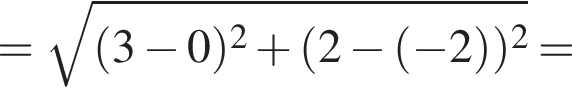
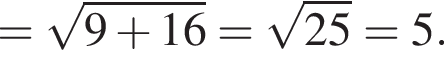
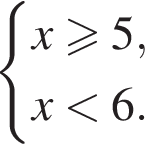

 получаем, что
получаем, что  следовательно, число
следовательно, число 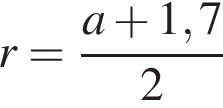
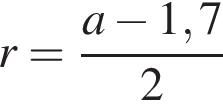
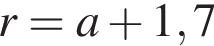
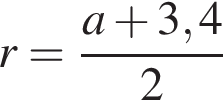
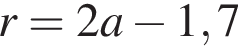
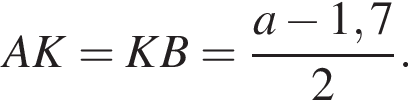
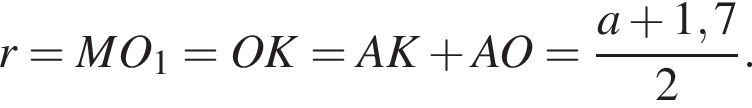
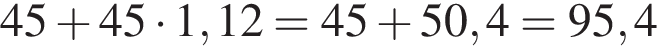 км.
км.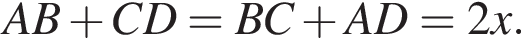 Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны.
Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны. 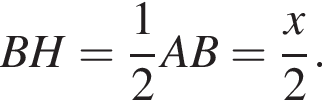 Поэтому из площади трапеции найдем x:
Поэтому из площади трапеции найдем x: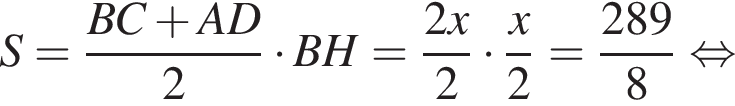
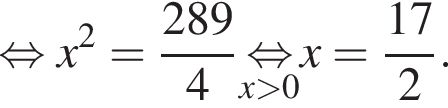
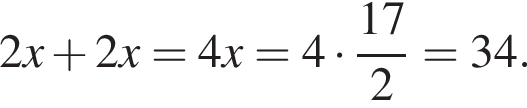
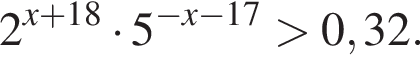
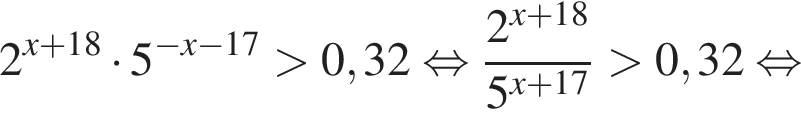
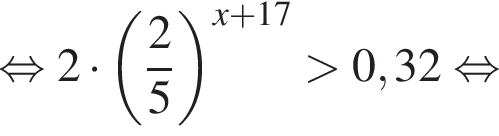
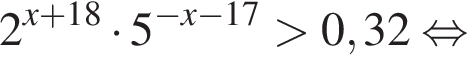
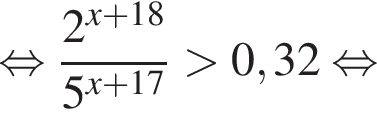
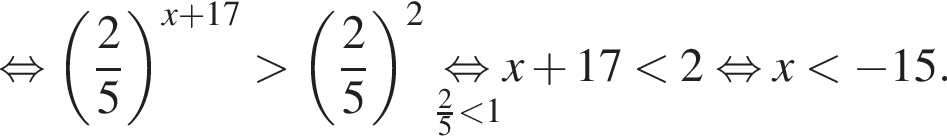
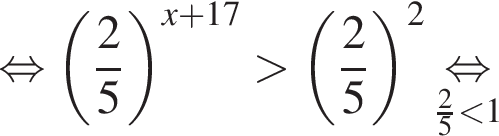
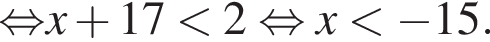
 с плоскостью основания (см. рис.) и отсекает часть NC1CA1D1D. Если объем призмы равен 48, то объем оставшейся части равен … .
с плоскостью основания (см. рис.) и отсекает часть NC1CA1D1D. Если объем призмы равен 48, то объем оставшейся части равен … .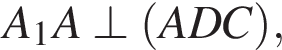
 следовательно, по теореме о трех перпендикулярах
следовательно, по теореме о трех перпендикулярах 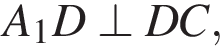 поэтому
поэтому  откуда
откуда 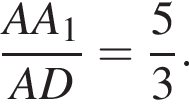 Пусть
Пусть 
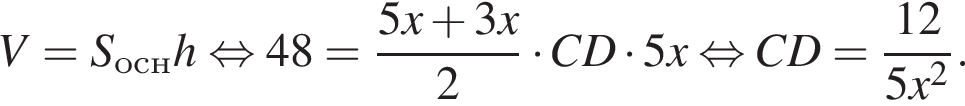
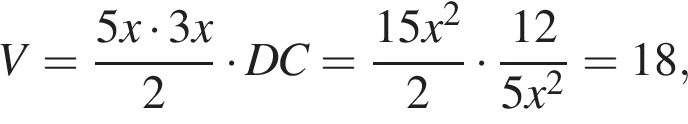 откуда
откуда 
 и заданной формулой
и заданной формулой 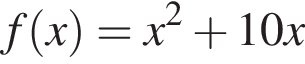 при
при 
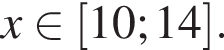
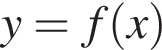 при
при 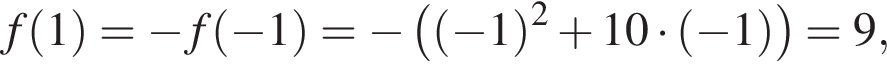
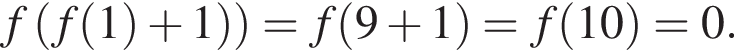 Утверждение 5 верно.
Утверждение 5 верно.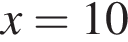 функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка
функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка 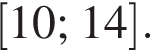 Утверждение 6 неверно.
Утверждение 6 неверно.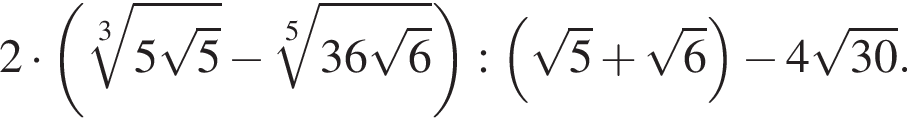
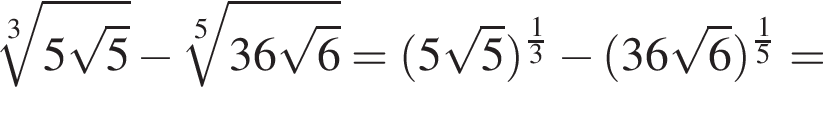
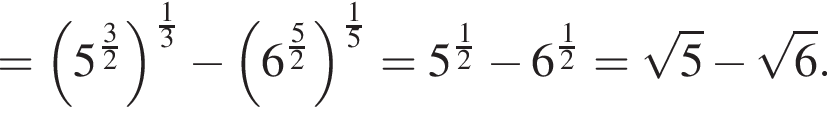
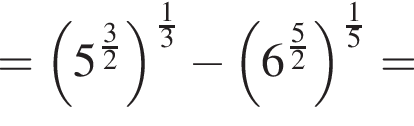
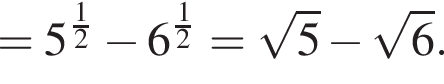
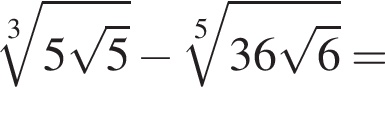
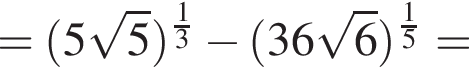
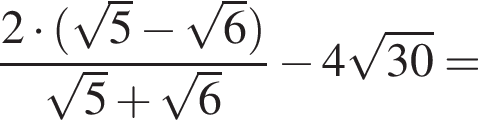
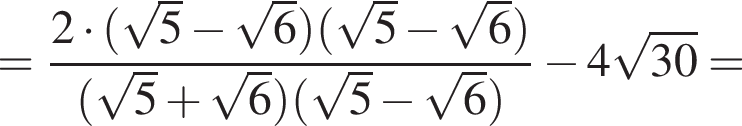
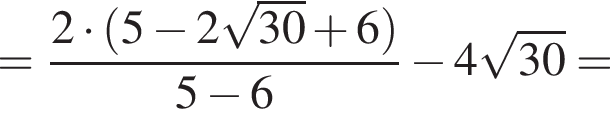
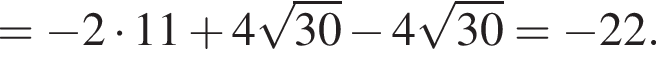

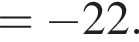
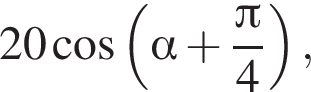 если
если 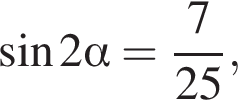
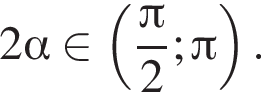
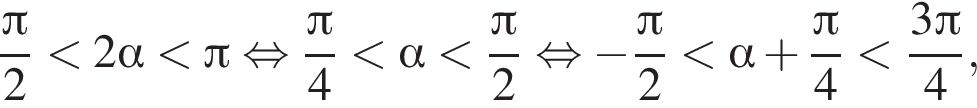

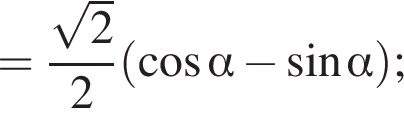
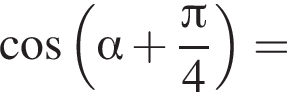
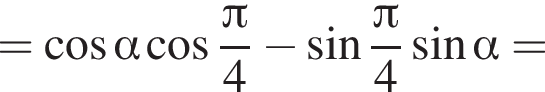
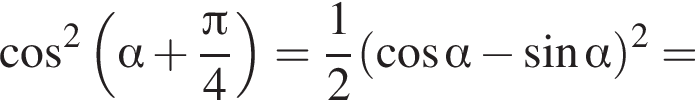

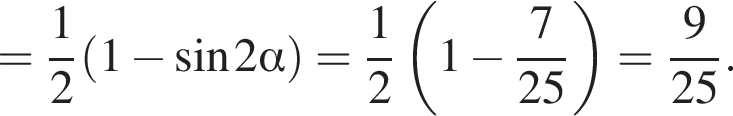
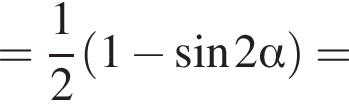
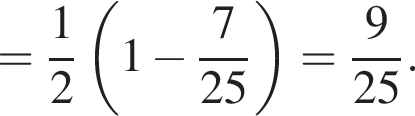
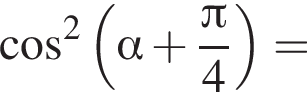
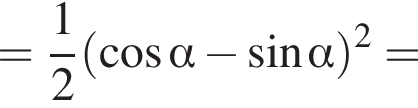
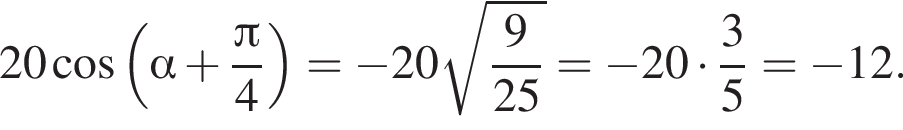
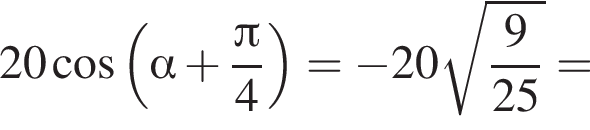
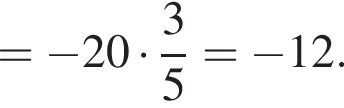
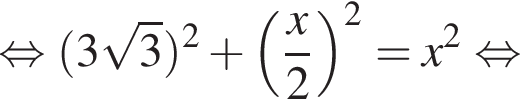
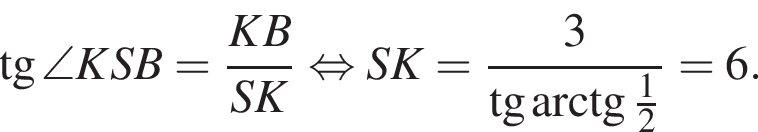 Площадь боковой поверхности равна
Площадь боковой поверхности равна 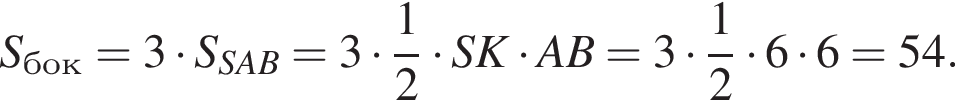
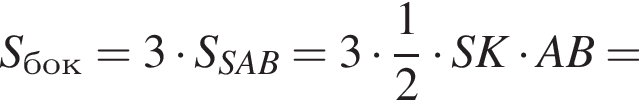
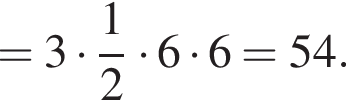
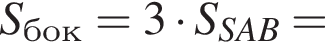
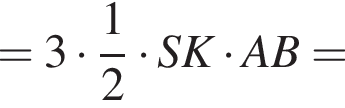
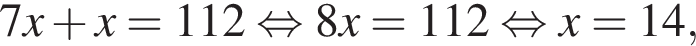
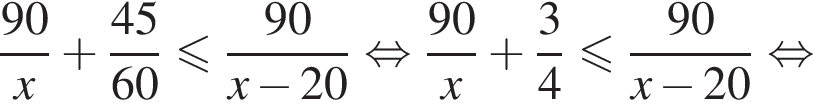

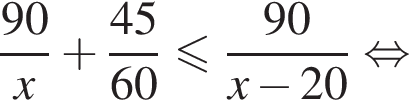
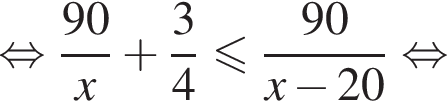
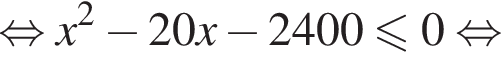

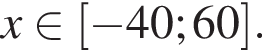 Таким образом, наибольшее значение скорости первого автомобиля — 60 км/ч.
Таким образом, наибольшее значение скорости первого автомобиля — 60 км/ч. и длины сторон KL и LN равны радиусу этой окружности. Найдите значение выражения S2, где S — площадь четырехугольника KMNL.
и длины сторон KL и LN равны радиусу этой окружности. Найдите значение выражения S2, где S — площадь четырехугольника KMNL. По теореме синусов:
По теореме синусов: 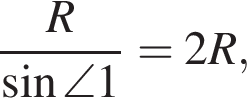 тогда
тогда 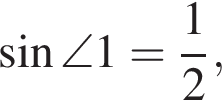 а значит,
а значит, 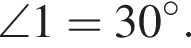 Кроме того, по свойствам вписанного четырехугольника,
Кроме того, по свойствам вписанного четырехугольника, 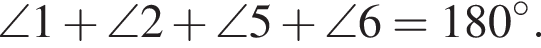 Тогда
Тогда 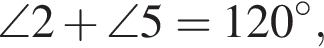 углы 2 и 5 равны как углы при основании равнобедренного треугольника KMN, а значит, каждый из них равен 60°. Таким образом, угол LKM, равный сумме углов 5 и 6, равен 90°, а значит, ML — диаметр. По теореме Пифагора в треугольнике LKM:
углы 2 и 5 равны как углы при основании равнобедренного треугольника KMN, а значит, каждый из них равен 60°. Таким образом, угол LKM, равный сумме углов 5 и 6, равен 90°, а значит, ML — диаметр. По теореме Пифагора в треугольнике LKM: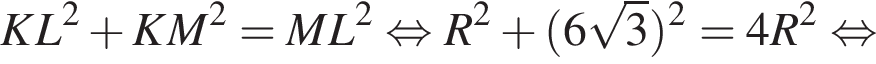
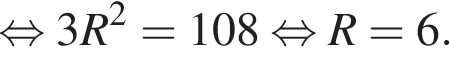
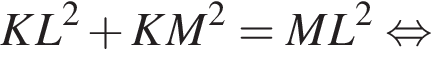
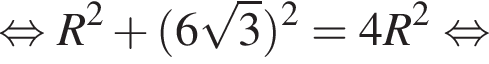
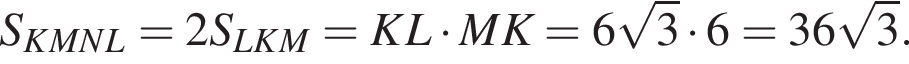

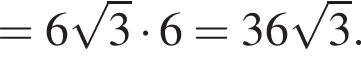

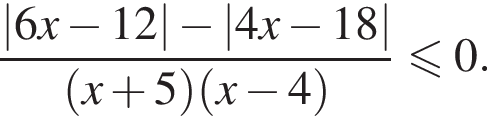
 совпадает со знаком разности
совпадает со знаком разности  имеем:
имеем: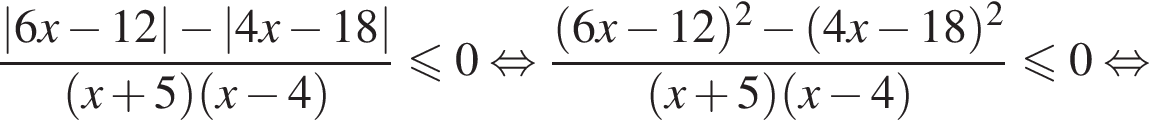
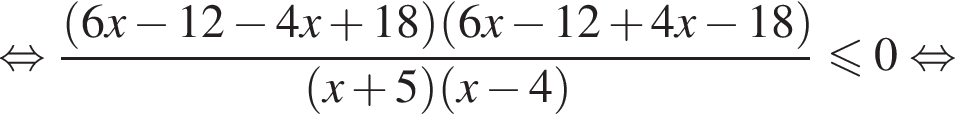
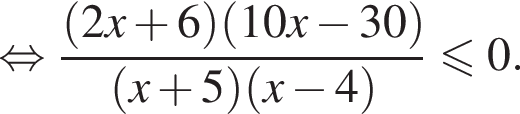
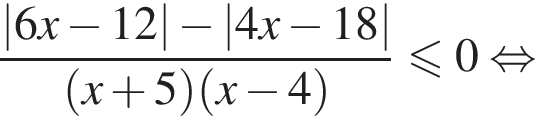
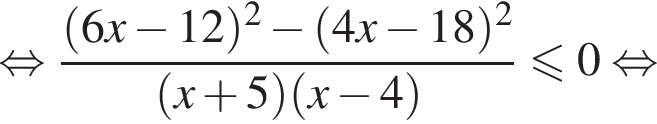
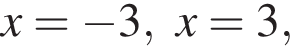 корни знаменателя
корни знаменателя 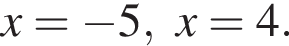 Поэтому:
Поэтому: 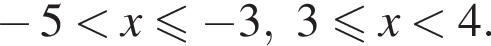 Целые решения — числа −4, −3, 3. Их сумма равна −4.
Целые решения — числа −4, −3, 3. Их сумма равна −4.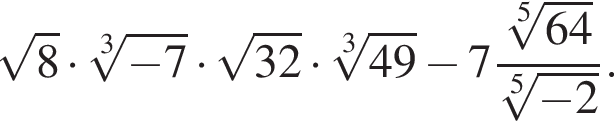
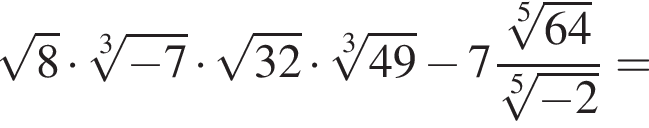
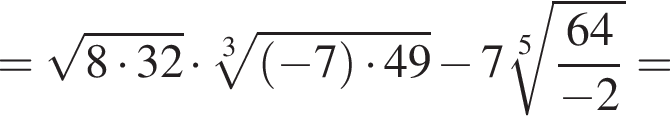
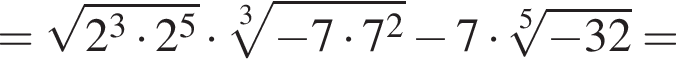
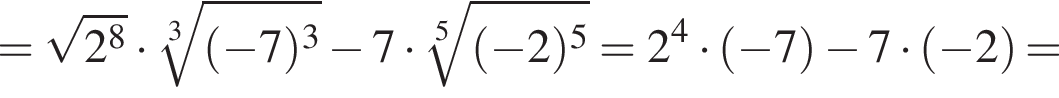
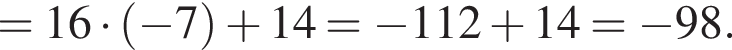
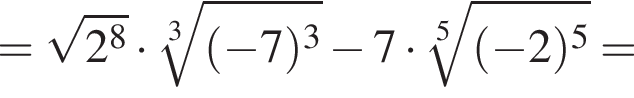
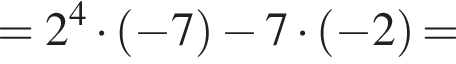
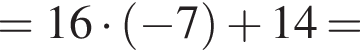

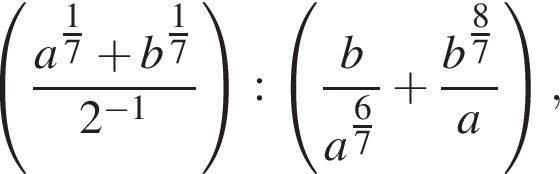 если a = 76, b = 8.
если a = 76, b = 8.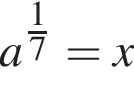 и
и 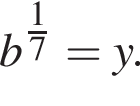 Тогда получим
Тогда получим 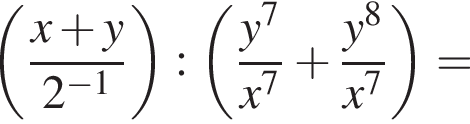
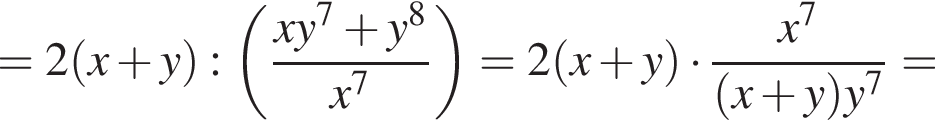
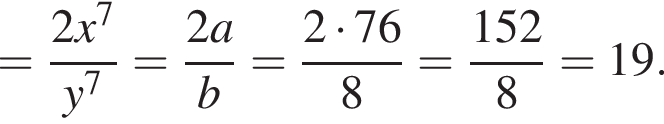
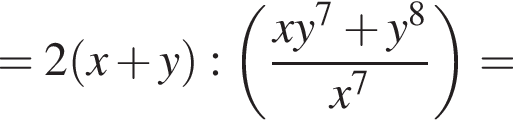
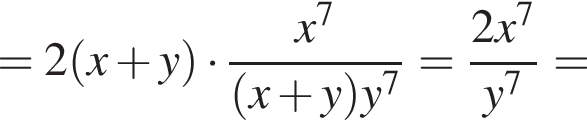
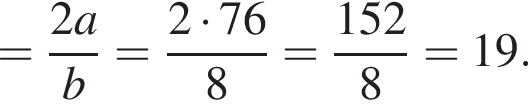
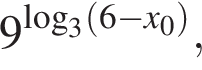 где x0 — корень уравнения
где x0 — корень уравнения 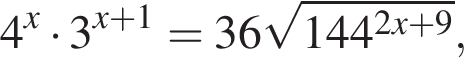 равно ... .
равно ... .
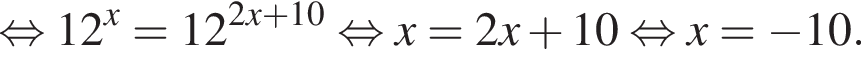
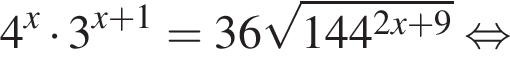
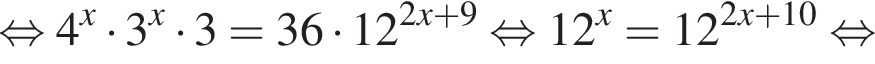
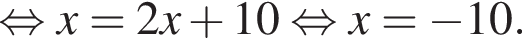
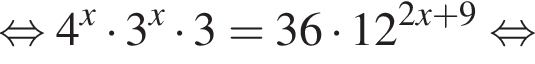
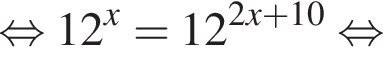
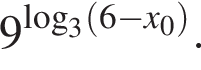 Получаем:
Получаем: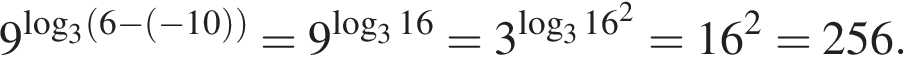
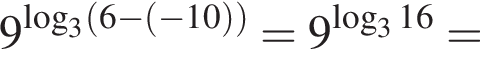
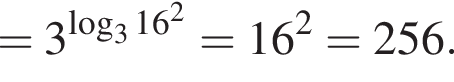
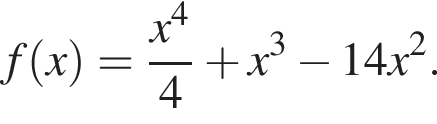
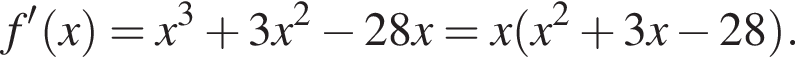
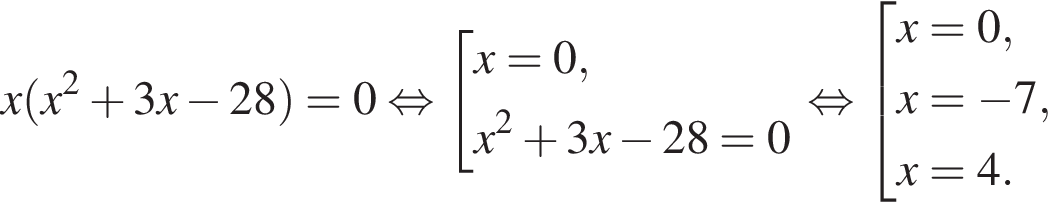
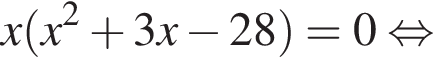
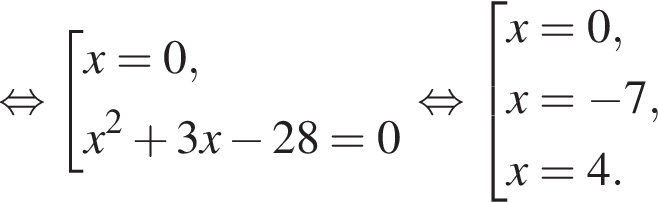
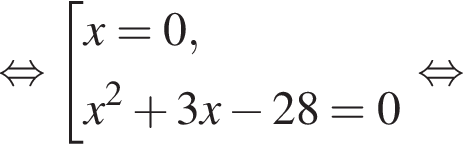
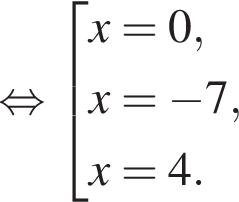
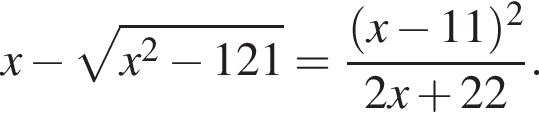
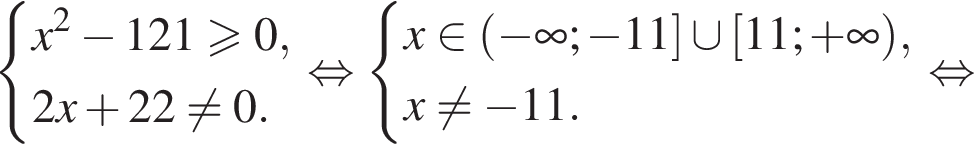
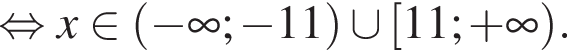
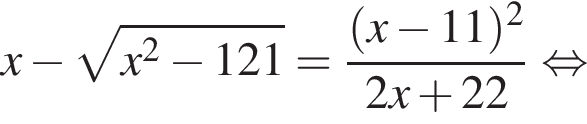
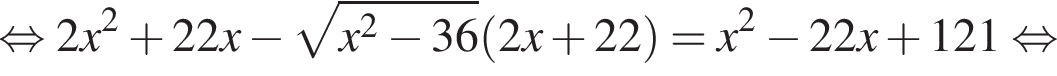
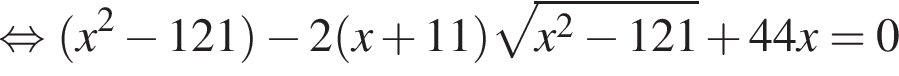
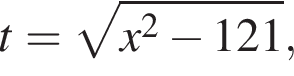 тогда
тогда 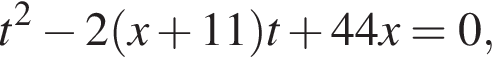 откуда
откуда 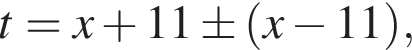 то есть
то есть 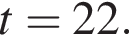

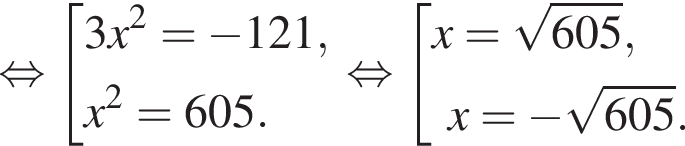

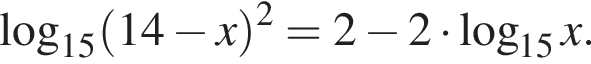
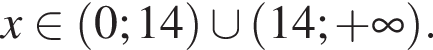 На этой области произведем преобразования:
На этой области произведем преобразования: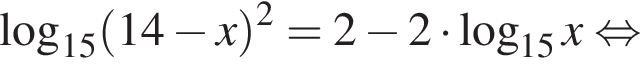
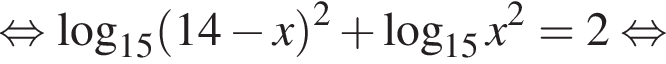
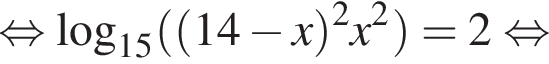

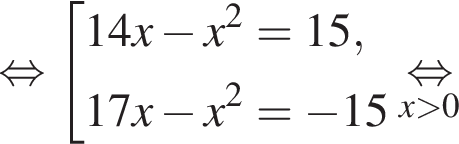
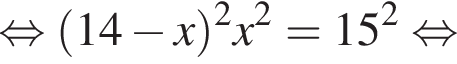
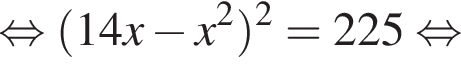
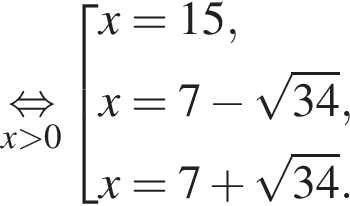

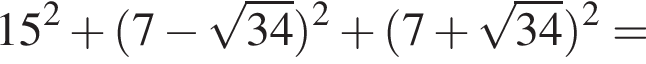
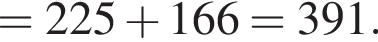

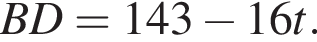 Тогда:
Тогда: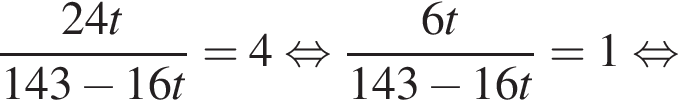
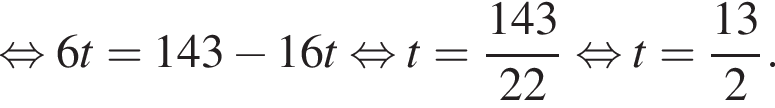
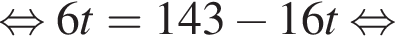
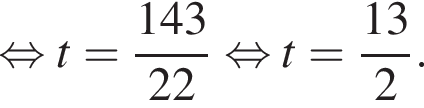
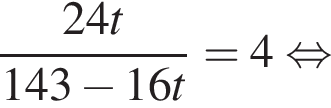
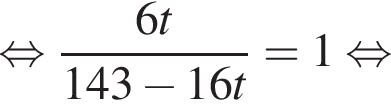
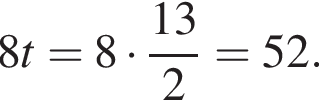
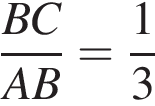 и
и 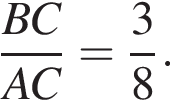 По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 11 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 11 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В? По свойству биссектрисы получаем, что
По свойству биссектрисы получаем, что 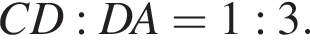 Значит, если
Значит, если  то
то 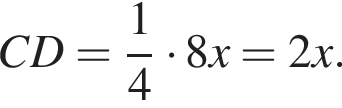
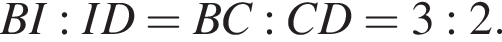 Значит, можно считать, что скорость первого тела равна 3υ, а второго 2υ. Время движения обратно пропорционально скорости, из условия следует, что
Значит, можно считать, что скорость первого тела равна 3υ, а второго 2υ. Время движения обратно пропорционально скорости, из условия следует, что 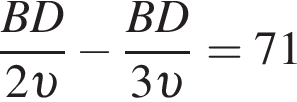
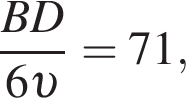 откуда
откуда